It's a classic interview question: what was the most difficult bug you ever fixed? In my case, the bug gave me a lot of trouble, and for a curious reason: the bug was not in the code, instead it was between the chair and the keyboard!
This story takes place in 1998. At the time, I was writing BrMSX, the first Brazilian MSX emulator (if you're not familiar with MSX, it was an 8-bit computer popular in East Asia, Europe and South America). I was taking extra care in the implementation: the emulator should be fast enough to run at full speed in the machines available at the time, and had to be precise enough to be indistinguishable from a real MSX.
The first objective was reached by writing the emulator in Assembly, the second by using a solid testing methodology. I didn't know about unit testing yet, but for each new feature, I always wrote a test program, and compared the program output in the emulator and in a real machine.
Early versions of my emulator were mute, I was only emulating the CPU and the video chip. When those two were stable, I started writing emulation of the audio chip: the AY-3-8912 from General Instrument, also known as PSG. This chip has three sound channels and one noise channel, the noise was used to make sound effects (such as gunshots and explosions), and also to make percussion sounds (such as drums).
To check if my noise implementation was correct, I made the following MSX BASIC code:
The magic numbers in code are scary, but their meanings are simple: register 7 is the mixer, a value of 183 turn on the noise generator in channel A, and turn off all the rest. Register 8 is the volume of channel A, setting it to 15 is the maximum volume. Finally, there's a loop changing the value of register 6, which is the noise frequency.
We expect this program to play some noise with a constant volume, at first with a low pitch, and then gradually becoming a higher pitch. That's in theory. On practice, however, something else happened!
I've redone the experiment and recorded it. On the video below, you can listen to the program running on a real MSX, and then on my emulator (I used dosbox to compile the 1998 version, before the bug was fixed).
How curious: even though I have set the volume to be constant, on a real MSX the volume gets lower at the end. Worse, on the emulator that doesn't happen!
That's a very subtle volume change, was I mistaken? To confirm, I've captured both signals and plotted them on Octave (in 1998 Octave didn't exist yet, so I used Matlab instead).
It looks like the turboR volume is really decreasing, but it's hard to compare. A better comparison can be made by noticing that the perception of loudness is physically caused by the power of the signal. And power is just the integral of the waveform squared. Drawing this on Octave we have:
There it is! I wasn't mistaken, in the last two steps the volume on the turboR really gets lower. But why does it happen? Maybe I could find out by analyzing the internals of the hardware.
In order to understand how the PSG works, it's useless to get the schematics of the MSX, or the datasheet of the AY-3-8912, because none of them explains what happens inside the chip. In theory I could open the chip and try to read the die using an electronic microscope, but since I didn't have access to one, I had to resort to reverse engineering.
It was easy to come up with a model for the PSG sound channels. It has three square wave generators, each one of that working like the diagram below:
The input clock of the counter is the MSX clock divided by 16, so it has 223506Hz. On each pulse, the counter increments by one, and the result is compared with the value of the frequency register. When the values are equal, the counter resets, and a T-type flip-flop invert state, generating the desired square wave.
What about the noise generator? At the time no one knew how it worked, some guessed it was thermal noise on some resistor, others guessed it was shot noise on some semiconductor junction.
The truth was easier than that, the PSG used a pseudo-random generator! In fact, it has a square wave generator just like the one above, and, on each output transition, it made a transition on a Linear Feedback Shift Register.
We know that every LFSR generates a periodic signal, so by capturing an entire period of the generator, we could deduce the exact characteristic polynomial used. Turns out it is x17+x14+1, the maximal polynomial of size 17.
So I knew how the signal was generated, and I even knew the exact LFSR used by the PSG. However, this knowledge didn't help to explain why the volume was getting lower. Perhaps I had an error in my implementation?
One of my requirements was to run the emulator at full-speed, in the machines of the time. By 1998, this means simulating this entire circuit on a Pentium 1, and yet still have time for the emulation of the CPU and the VDP. Coding this in Assembly wasn't enough, I had to guarantee that all inner loops ran entirely in registers.
That's hard to achieve in the x86 architecture, which has only 7 general-purpose registers. My first attempt was a hack: during PSG emulation, I turned off all interrupts, and used the stack pointer as a register. This worked fine at home, but I used DOS at home. Most of my users had Windows 95, and this hack didn't work there.
Let's find another solution: there were lots of variables which changed when a PSG register is touched, but have constants values inside the inner loop. This presented a good opportunity to use self-modifiable code: I would "recompile" the inner loop every time a PSG register changed. This solution worked on Windows, and it was fast enough.
Fast, but also complex. You can see this code in github, it's neither legible, not easy to understand. Perhaps the volume wasn't changing due to bug in the implementation.
However, after thinking about it, I came to the conclusion that my implementation should be correct. If the implementation was wrong, then this error should only appear in my emulator. But all other MSX emulators had the same bug!
If many different implementation had the same bug, then the problem clearly wasn't in the code. It must be something more abstract. Maybe I could get some clue by analyzing mathematically the signal.
Let's model the signal: suppose the output bits of the LFSR are a discrete sequence {di}, and for each bit 1 on the input we output a waveform s(t). If the pulse width is T, then the PSG noise is:
From the theory of stochastic processes, we know that the power spectral density of the signal is:
...where Gd(f) is the power spectral density of the sequency {di}, and S(f) is the Fourier transform of s(t). If we suppose the noise is white noise, then Gd(f) is a constant. The waveform s(t) is a rectangular pulse, whose transform is the sinc function. Therefore, the power spectral density of the signal is a squared sinc.
The bug appears when PSG register has the value 1, in this case T=8.98µs. The power spectral density of the output is:
Again, the perceptual loudness of the output is the power of the signal, and by Parseval's theorem, the power is the area below the graph.
After staring for some time at this graph, I had the insight I was looking for!
The problem was between the chair and the keyboard! More specifically, the problem happened because there was a human being between the chair and the keyboard! The human auditory system can only hear frequencies up to 20kHz, and this signal was spreading power over inaudible frequencies. A human being can only hear this part of the power:
The integral of the squared sinc cannot be solved analytically, but we can evaluate it numerically. This is a table with the audible power divided by the total power, for each of the frequency values used by the BASIC program:
Comparing the power of the emulator and the turboR on the graph, it clear that this percentage is exactly what's missing to make the emulator sound the same as the real machine. By adding this attenuation to the emulator, it became true to the original as I wanted.
If you're paying attention, you may be asking yourself: "If the problem is only perceptual, then why the graph of the power measured by Octave shows the volume loss?". This is also an artifact from the human auditory system, but indirectly so.
When I plugged the turboR on my notebook's microphone, the sound board made the audio capture with CD quality, sampling it at 44100Hz. The designers of the sound card are smart, so they added a low-pass filter on the Nyquist's frequency before sampling, to avoid aliasing. Since this frequency was calculated to throw away everything humans can't hear, we're back to the same problem.
If you want to make the experiment yourself, I've placed on github the Octave scripts used to generate the images and tables of this post:
Scripts in Octave for noise analysis
This bug gave me lot of trouble to solve, but, in the end, I doubt anyone but me noticed the difference :)
The Story
The first objective was reached by writing the emulator in Assembly, the second by using a solid testing methodology. I didn't know about unit testing yet, but for each new feature, I always wrote a test program, and compared the program output in the emulator and in a real machine.
Early versions of my emulator were mute, I was only emulating the CPU and the video chip. When those two were stable, I started writing emulation of the audio chip: the AY-3-8912 from General Instrument, also known as PSG. This chip has three sound channels and one noise channel, the noise was used to make sound effects (such as gunshots and explosions), and also to make percussion sounds (such as drums).
To check if my noise implementation was correct, I made the following MSX BASIC code:
10 SOUND 7,183 20 SOUND 8,15 30 FOR I=8 TO 1 STEP -1 40 SOUND 6,I 50 PRINT I 60 FOR J=0 TO 300: NEXT J,I
70 BEEP
The magic numbers in code are scary, but their meanings are simple: register 7 is the mixer, a value of 183 turn on the noise generator in channel A, and turn off all the rest. Register 8 is the volume of channel A, setting it to 15 is the maximum volume. Finally, there's a loop changing the value of register 6, which is the noise frequency.
We expect this program to play some noise with a constant volume, at first with a low pitch, and then gradually becoming a higher pitch. That's in theory. On practice, however, something else happened!
The Bug
I've redone the experiment and recorded it. On the video below, you can listen to the program running on a real MSX, and then on my emulator (I used dosbox to compile the 1998 version, before the bug was fixed).
How curious: even though I have set the volume to be constant, on a real MSX the volume gets lower at the end. Worse, on the emulator that doesn't happen!
That's a very subtle volume change, was I mistaken? To confirm, I've captured both signals and plotted them on Octave (in 1998 Octave didn't exist yet, so I used Matlab instead).
It looks like the turboR volume is really decreasing, but it's hard to compare. A better comparison can be made by noticing that the perception of loudness is physically caused by the power of the signal. And power is just the integral of the waveform squared. Drawing this on Octave we have:
There it is! I wasn't mistaken, in the last two steps the volume on the turboR really gets lower. But why does it happen? Maybe I could find out by analyzing the internals of the hardware.
The Circuit
In order to understand how the PSG works, it's useless to get the schematics of the MSX, or the datasheet of the AY-3-8912, because none of them explains what happens inside the chip. In theory I could open the chip and try to read the die using an electronic microscope, but since I didn't have access to one, I had to resort to reverse engineering.
It was easy to come up with a model for the PSG sound channels. It has three square wave generators, each one of that working like the diagram below:
The input clock of the counter is the MSX clock divided by 16, so it has 223506Hz. On each pulse, the counter increments by one, and the result is compared with the value of the frequency register. When the values are equal, the counter resets, and a T-type flip-flop invert state, generating the desired square wave.
What about the noise generator? At the time no one knew how it worked, some guessed it was thermal noise on some resistor, others guessed it was shot noise on some semiconductor junction.
The truth was easier than that, the PSG used a pseudo-random generator! In fact, it has a square wave generator just like the one above, and, on each output transition, it made a transition on a Linear Feedback Shift Register.
We know that every LFSR generates a periodic signal, so by capturing an entire period of the generator, we could deduce the exact characteristic polynomial used. Turns out it is x17+x14+1, the maximal polynomial of size 17.
So I knew how the signal was generated, and I even knew the exact LFSR used by the PSG. However, this knowledge didn't help to explain why the volume was getting lower. Perhaps I had an error in my implementation?
The Implementation
One of my requirements was to run the emulator at full-speed, in the machines of the time. By 1998, this means simulating this entire circuit on a Pentium 1, and yet still have time for the emulation of the CPU and the VDP. Coding this in Assembly wasn't enough, I had to guarantee that all inner loops ran entirely in registers.
That's hard to achieve in the x86 architecture, which has only 7 general-purpose registers. My first attempt was a hack: during PSG emulation, I turned off all interrupts, and used the stack pointer as a register. This worked fine at home, but I used DOS at home. Most of my users had Windows 95, and this hack didn't work there.
Let's find another solution: there were lots of variables which changed when a PSG register is touched, but have constants values inside the inner loop. This presented a good opportunity to use self-modifiable code: I would "recompile" the inner loop every time a PSG register changed. This solution worked on Windows, and it was fast enough.
Fast, but also complex. You can see this code in github, it's neither legible, not easy to understand. Perhaps the volume wasn't changing due to bug in the implementation.
However, after thinking about it, I came to the conclusion that my implementation should be correct. If the implementation was wrong, then this error should only appear in my emulator. But all other MSX emulators had the same bug!
If many different implementation had the same bug, then the problem clearly wasn't in the code. It must be something more abstract. Maybe I could get some clue by analyzing mathematically the signal.
The Transform
Let's model the signal: suppose the output bits of the LFSR are a discrete sequence {di}, and for each bit 1 on the input we output a waveform s(t). If the pulse width is T, then the PSG noise is:
From the theory of stochastic processes, we know that the power spectral density of the signal is:
...where Gd(f) is the power spectral density of the sequency {di}, and S(f) is the Fourier transform of s(t). If we suppose the noise is white noise, then Gd(f) is a constant. The waveform s(t) is a rectangular pulse, whose transform is the sinc function. Therefore, the power spectral density of the signal is a squared sinc.
The bug appears when PSG register has the value 1, in this case T=8.98µs. The power spectral density of the output is:
Again, the perceptual loudness of the output is the power of the signal, and by Parseval's theorem, the power is the area below the graph.
After staring for some time at this graph, I had the insight I was looking for!
The solution
The problem was between the chair and the keyboard! More specifically, the problem happened because there was a human being between the chair and the keyboard! The human auditory system can only hear frequencies up to 20kHz, and this signal was spreading power over inaudible frequencies. A human being can only hear this part of the power:
The integral of the squared sinc cannot be solved analytically, but we can evaluate it numerically. This is a table with the audible power divided by the total power, for each of the frequency values used by the BASIC program:
| Register 6 | Percentage of audible power |
| 8 | 0.99 |
| 7 | 0.99 |
| 6 | 0.99 |
| 5 | 0.99 |
| 4 | 0.99 |
| 3 | 0.96 |
| 2 | 0.83 |
| 1 | 0.50 |
Comparing the power of the emulator and the turboR on the graph, it clear that this percentage is exactly what's missing to make the emulator sound the same as the real machine. By adding this attenuation to the emulator, it became true to the original as I wanted.
If you're paying attention, you may be asking yourself: "If the problem is only perceptual, then why the graph of the power measured by Octave shows the volume loss?". This is also an artifact from the human auditory system, but indirectly so.
When I plugged the turboR on my notebook's microphone, the sound board made the audio capture with CD quality, sampling it at 44100Hz. The designers of the sound card are smart, so they added a low-pass filter on the Nyquist's frequency before sampling, to avoid aliasing. Since this frequency was calculated to throw away everything humans can't hear, we're back to the same problem.
If you want to make the experiment yourself, I've placed on github the Octave scripts used to generate the images and tables of this post:
Scripts in Octave for noise analysis
This bug gave me lot of trouble to solve, but, in the end, I doubt anyone but me noticed the difference :)






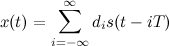
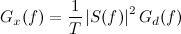



No comments:
Post a Comment