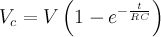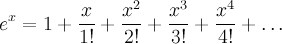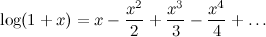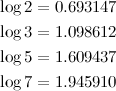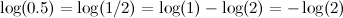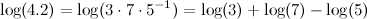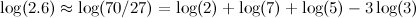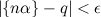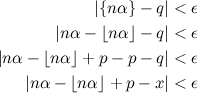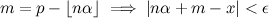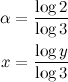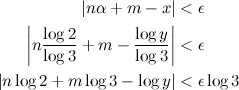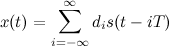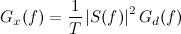Some time ago I was asked if there's a way to be more creative. This is quite difficult to find out: in order to know if a method works or not, you would have to measure creativity before and after the method, and not one knows how to measure creativity.
Having said that, I know some tricks that work quite well. On this post, I'll talk about one such method, by telling a story that happened to me back when I was a kid studying electronics.
In 1991 I started a three-year electronics course on one of the best schools in my city. On the first day I was given a shopping list with things I should buy, to use during the classes. There was the basic stuff such as pencils and notebooks, but also items such as a Rapidograf pen, a Leroy pantograph and a scientific calculator.
The last item was a problem. At that time, scientific calculators were expensive (actually, even today they are expensive). Since I had no money to buy one, I decided to complete the course using only a four-operations calculator.
The first year of the course was easy, since the only component used was the resistor, and calculations with resistors can be done with just the four basic operations. On the second year the capacitor was introduced, and then things got complicated: I had to make calculations using exponentials and trigonometric functions, which my calculator of course didn't support.
So what should I do? Since I knew no one who could lend me a scientific calculator, and I had no money to buy one, I had to resort to the inheritance from my grandpa.
My grandpa didn't leave me money or lands. Instead, he left me knowledge! A very large bookcase, from wall to wall, with old books from the 60s, covering all kinds of topics. The book that saved me was a very curious collection of Mathematics for Theologicians. I'm not exactly sure why a priest needs to know mathematics, but the book was very complete, going from notable products all the way up to Calculus. And right there on the middle there was the trick that I needed.
The problems I had to solve were like this: given the RC-series circuit below, calculate the voltage on the capacitor after 2 seconds.
This course was not university-level, it was meant to train technicians. This means I didn't have to solve the differential equation, the formula was given and I just needed to apply it:
My problem was the exponential, only present in scientific calculators. Using the book from the theologicians, however, I discovered the formula that solved my problem: the expansion in Taylor's series:
It looks complicated, but this formula can be used quite easily in a four-operations calculator, as long as it has memory buttons (M+, M-, MC and MR). In the given example, I needed to calculate exp(-0.2) with a short sequence of button presses:
With 29 touches I got the value of 0.818, correct up to three digits (and the professor only asked for two). If you have agile fingers, you'll spend a very short time on this!
This method is also good for sines and cosines, used on the calculations of angles of fasors and of the power factor. But there's a case where this method doesn't work...
Sometimes the exercise would ask for the inverse problem: given the same RC-series circuit, how much time does it take for the capacitor to have half the voltage of the source? In this case, the calculations depend on log(0.5), and there's no logarithm on the four-operations calculator.
Even worse, in this case the book also didn't help. The only formula available on the the book was:
If you try to use this formula in your calculator, you'll see it's not practical: many terms are needed to get the two-digit precision needed. You can estimate the convergence speed of the formula by looking at its coefficients: on the exponential, the coefficients falls down with the speed of the factorial, and on the logarithm they fall down with the speed of the harmonic series, which is much slower.
Nowadays, I would use Newton-Raphson method to calculate the logarithm. But at that time I didn't know anything about numerical methods. So I had to improvise. Instead of memorizing a formula, I memorized four numbers:
Memorizing seven-digit number is not so difficult, we do that all the time with telephone numbers. And with there four numbers, I could calculate everything I needed! So do you need log(0.5)?
Let's say you now need log(4.2):
What about log(2.6)? Oops, 26 has a prime factor of 13 that I don't have on my table. But I can approximate it:
The result is not exact, but it's correct up to two digits. Who needs a scientific calculator after all?
Was this luck, or can I always approximate a value using the numbers I memorized? At the time I had an intuition that this was the case, but nowadays I prove it's true! The proof is on the blue box below, skip it if you're not familiar with number theory:
I could end this post with a conclusion like "if life has given you lemons, find some copper bars and make a battery". Instead, there is a more important lesson. Marissa Mayer said in an interview in 2006: creativity loves restrictions, specially if paired with a healthy disregard for the impossible.
Try to remember something that you have seen and found very creative. What about the artist that made portraits using cassete tapes? The guy who made art using fruits? The person who rewrote Poe's The Raven in a way that the number of letters of each word matched the digits of pi?
All of these are examples of the author has self-imposed a constraint (on form, on content, on used materials). If you want to enhance your creativity, adding constraints if more effective that removing them.
This is not true only for art, it's true for computing too. Try to make your software use less memory, less CPU, try to code the same thing in less time: this will force you to use more creative solutions.
(Thanks for the people on Math Stack Exchange for the help on the proof)
Having said that, I know some tricks that work quite well. On this post, I'll talk about one such method, by telling a story that happened to me back when I was a kid studying electronics.
Electronics school
The last item was a problem. At that time, scientific calculators were expensive (actually, even today they are expensive). Since I had no money to buy one, I decided to complete the course using only a four-operations calculator.
The first year of the course was easy, since the only component used was the resistor, and calculations with resistors can be done with just the four basic operations. On the second year the capacitor was introduced, and then things got complicated: I had to make calculations using exponentials and trigonometric functions, which my calculator of course didn't support.
So what should I do? Since I knew no one who could lend me a scientific calculator, and I had no money to buy one, I had to resort to the inheritance from my grandpa.
My grandpa didn't leave me money or lands. Instead, he left me knowledge! A very large bookcase, from wall to wall, with old books from the 60s, covering all kinds of topics. The book that saved me was a very curious collection of Mathematics for Theologicians. I'm not exactly sure why a priest needs to know mathematics, but the book was very complete, going from notable products all the way up to Calculus. And right there on the middle there was the trick that I needed.
The Exponential
The problems I had to solve were like this: given the RC-series circuit below, calculate the voltage on the capacitor after 2 seconds.
This course was not university-level, it was meant to train technicians. This means I didn't have to solve the differential equation, the formula was given and I just needed to apply it:
My problem was the exponential, only present in scientific calculators. Using the book from the theologicians, however, I discovered the formula that solved my problem: the expansion in Taylor's series:
It looks complicated, but this formula can be used quite easily in a four-operations calculator, as long as it has memory buttons (M+, M-, MC and MR). In the given example, I needed to calculate exp(-0.2) with a short sequence of button presses:
C
MC
1
M+
.
2
M-
×
.
2
÷
2
=
M+
×
.
2
÷
3
=
M-
×
.
2
÷
4
=
M+
MR
With 29 touches I got the value of 0.818, correct up to three digits (and the professor only asked for two). If you have agile fingers, you'll spend a very short time on this!
This method is also good for sines and cosines, used on the calculations of angles of fasors and of the power factor. But there's a case where this method doesn't work...
The Logarithm
Sometimes the exercise would ask for the inverse problem: given the same RC-series circuit, how much time does it take for the capacitor to have half the voltage of the source? In this case, the calculations depend on log(0.5), and there's no logarithm on the four-operations calculator.
Even worse, in this case the book also didn't help. The only formula available on the the book was:
If you try to use this formula in your calculator, you'll see it's not practical: many terms are needed to get the two-digit precision needed. You can estimate the convergence speed of the formula by looking at its coefficients: on the exponential, the coefficients falls down with the speed of the factorial, and on the logarithm they fall down with the speed of the harmonic series, which is much slower.
Nowadays, I would use Newton-Raphson method to calculate the logarithm. But at that time I didn't know anything about numerical methods. So I had to improvise. Instead of memorizing a formula, I memorized four numbers:
Memorizing seven-digit number is not so difficult, we do that all the time with telephone numbers. And with there four numbers, I could calculate everything I needed! So do you need log(0.5)?
Let's say you now need log(4.2):
What about log(2.6)? Oops, 26 has a prime factor of 13 that I don't have on my table. But I can approximate it:
The result is not exact, but it's correct up to two digits. Who needs a scientific calculator after all?
Was this luck, or can I always approximate a value using the numbers I memorized? At the time I had an intuition that this was the case, but nowadays I prove it's true! The proof is on the blue box below, skip it if you're not familiar with number theory:
The proof uses directly the Weyl's equidistribution theorem: the set of the fractional parts of the integer multiples of an irrational number is dense in [0,1). This means that for each irrational α and real q, where 0 ≤ q < 1,and for every positive ε,there is always an integer n such that the formula below is true:
With a little bit of algebra we can extend the range from [0,1) to all reals. Suppose we have a given x, such that x=p+q, where p is the integer part and q is the fractional part. From the equation above:
Notice that the floor of nα is an integer, and also p is an integer. Let's call m the difference of those integers:
This means that I can choose any irrational α and real x, and there will be always a pair of integers m and n satisfying this equation. Since I can choose any numbers, I'll choose α and x as below:
Since α is irrational, we can use our inequation:
And there we go: we can always approximate the log of a given real y as the sum of integer multiples of log(2) and log(3). I didn't even had to memorize log(5) and log(7)!
Unfortunately, this is an example of a non-constructible proof: it can guarantee these integers m and n exist, but it doesn't tell us how to choose them. In the end, you'll have to choose them using your intuition, just like I used to do :)
With a little bit of algebra we can extend the range from [0,1) to all reals. Suppose we have a given x, such that x=p+q, where p is the integer part and q is the fractional part. From the equation above:
Notice that the floor of nα is an integer, and also p is an integer. Let's call m the difference of those integers:
This means that I can choose any irrational α and real x, and there will be always a pair of integers m and n satisfying this equation. Since I can choose any numbers, I'll choose α and x as below:
Since α is irrational, we can use our inequation:
And there we go: we can always approximate the log of a given real y as the sum of integer multiples of log(2) and log(3). I didn't even had to memorize log(5) and log(7)!
Unfortunately, this is an example of a non-constructible proof: it can guarantee these integers m and n exist, but it doesn't tell us how to choose them. In the end, you'll have to choose them using your intuition, just like I used to do :)
Creativity
I could end this post with a conclusion like "if life has given you lemons, find some copper bars and make a battery". Instead, there is a more important lesson. Marissa Mayer said in an interview in 2006: creativity loves restrictions, specially if paired with a healthy disregard for the impossible.
Try to remember something that you have seen and found very creative. What about the artist that made portraits using cassete tapes? The guy who made art using fruits? The person who rewrote Poe's The Raven in a way that the number of letters of each word matched the digits of pi?
All of these are examples of the author has self-imposed a constraint (on form, on content, on used materials). If you want to enhance your creativity, adding constraints if more effective that removing them.
This is not true only for art, it's true for computing too. Try to make your software use less memory, less CPU, try to code the same thing in less time: this will force you to use more creative solutions.
(Thanks for the people on Math Stack Exchange for the help on the proof)



.jpg)